Una pequeña historia
Hace algún tiempo, vi un vídeo en el que un chico explicaba cómo un estudiante de matemáticas logró aprobar un examen gracias a un problema de programación.
El estudiante recibió una nota de 4.9 en su examen y pidió al profesor que le aprobara puesto que solo le quedaba una décima para ello. Este le respondió que, si lo hacía, tendría que hacer lo mismo con el resto.
Así que el alumno le propuso al profesor que pusiera detrás del 4.9 muchos números al guardarlo en el sistema.
El maestro le dijo que eso seguiría siendo un suspenso. Él aceptó la propuesta.
Al recibir el boletín de calificaciones, el estudiante vió que la asignatura en la que había obtenido un 4.9 ahora reflejaba un 5. Se había beneficiado de uno de los problemas de la programación: el redondeo de números con coma flotante.
Esto me ha llevado a hablar sobre este tema.
¿Por qué ocurre esto?
Porque los ordenadores trabajan en binario y nosotros lo hacemos en decimal, lo que produce un error a la hora de redondear y almacenar el número.
Por ejemplo, cuando nosotros queremos calcular el valor de la fracción 1/3, en base 10, su valor se puede aproximar cómo 0.3, 0.33, 0.333, etc., pero nunca será exacto.
Lo mismo pasa en los ordenadores aunque trabajen en binario,es decir, utilizando base 2, la fracción 1/10 nunca valdrá exactamente 0.1 en base 2.

Resultado:

Por lo tanto, hay que tener en cuenta que las operaciones aritméticas son binarias no decimales, y cada operación realizada sufre un nuevo error de redondeo.
Esto ocurre independientemente del lenguaje de programación que utilicemos.
¿Por qué es un problema?
Esto nos ocasiona un problema cuando estamos manejando cantidades muy precisas, como cuando queremos calcular precios, realizar calibraciones de maquinaria, etc…, ya que en muchas ocasiones tener una desviación de centésimas, milésimas o millonésimas es inaceptable.
Veamos unos ejemplos de redondeo
Vamos a redondear los siguientes números a 2 decimales:
- 0.875
- 0.345
- 0.335
- 17.515
- 245.515
Tomando en cuenta la siguiente premisa:
Cuando el número que esté a la derecha del decimal a redondear sea par, se redondeará a la baja y cuando ese mismo número sea impar se redondeará al alza.
Vamos a ver que pasa:
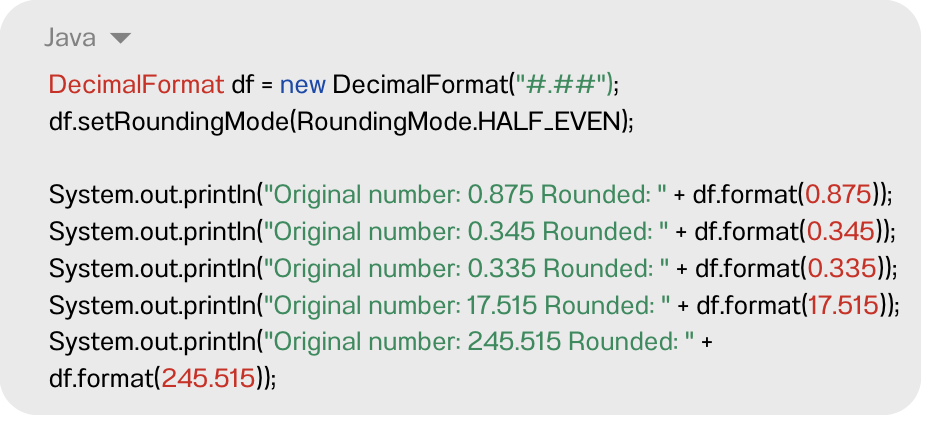
Respuesta:

Si nos fijamos, todos los números se han redondeado cumpliendo la premisa, excepto el último, pero, ¿por qué?
Esto ocurre, porque esos no son los números que el sistema está tratando en realidad, son estos:
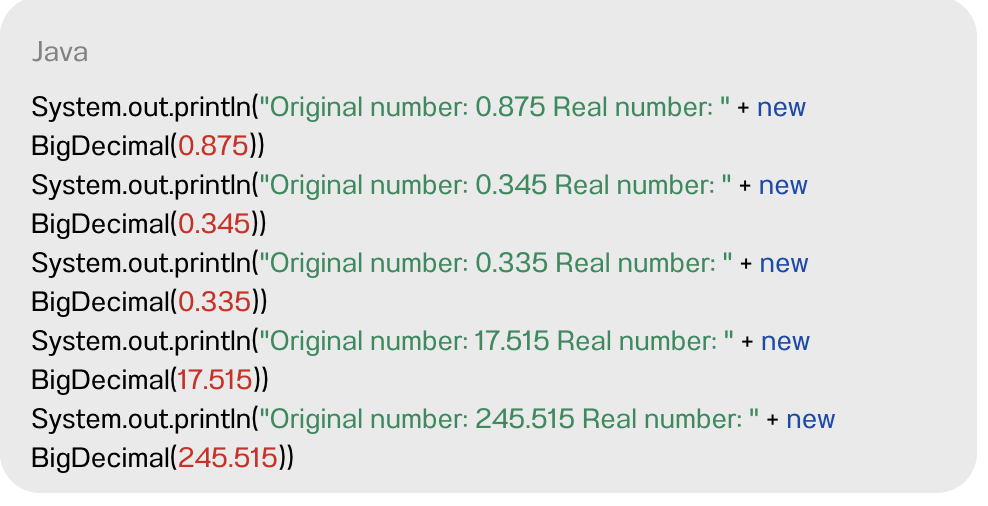
Respuesta:

¿Cómo lo solucionamos?
En el caso de Java, lo podemos solucionar utilizando java.math.BigDecimal, pasando en el constructor el número como cadena, ya que de esa forma utilizará el número exactamente que queremos.
La otra alternativa es utilizar el método BigDecimal.valueOf (double), ya que internamente convierte el número a cadena, obteniendo el mismo resultado que con la opción anterior.


Respuesta:

En Javascript, existe la librería bigdecimal.js para atajar el problema y en Python el módulo decimal.
Fuentes
https://docs.oracle.com/cd/E19957-01/806-3568/ncg_goldberg.html
https://www.geeksforgeeks.org/ieee-standard-754-floating-point-numbers/
https://trinistorm.org/wrong-results-from-floating-point-arithmetic/
https://docs.oracle.com/javase/7/docs/api/java/math/BigDecimal.html#BigDecimal(double)
https://docs.python.org/3.11/library/decimal.html
https://mikemcl.github.io/bignumber.js/

